問題概要

$R$行$C$列のグリッド上を, 上下左右の移動を繰り返すことで全て$K$回ずつ訪れることは可能か判定しなさい.

制約

• $1 \leq R \leq 50$
• $1 \leq C \leq 50$
• $1 \leq K \leq 50$

考察

歪な形じゃないので, $K = 1$のときは自明に可能.

$K > 1$のときは, 始点と終点が隣りあってれば大丈夫.

下のどっちかだったら確実に大丈夫だけど, これ以外に無いことは証明できず… (コンテスト中に証明するの厳しくないか)

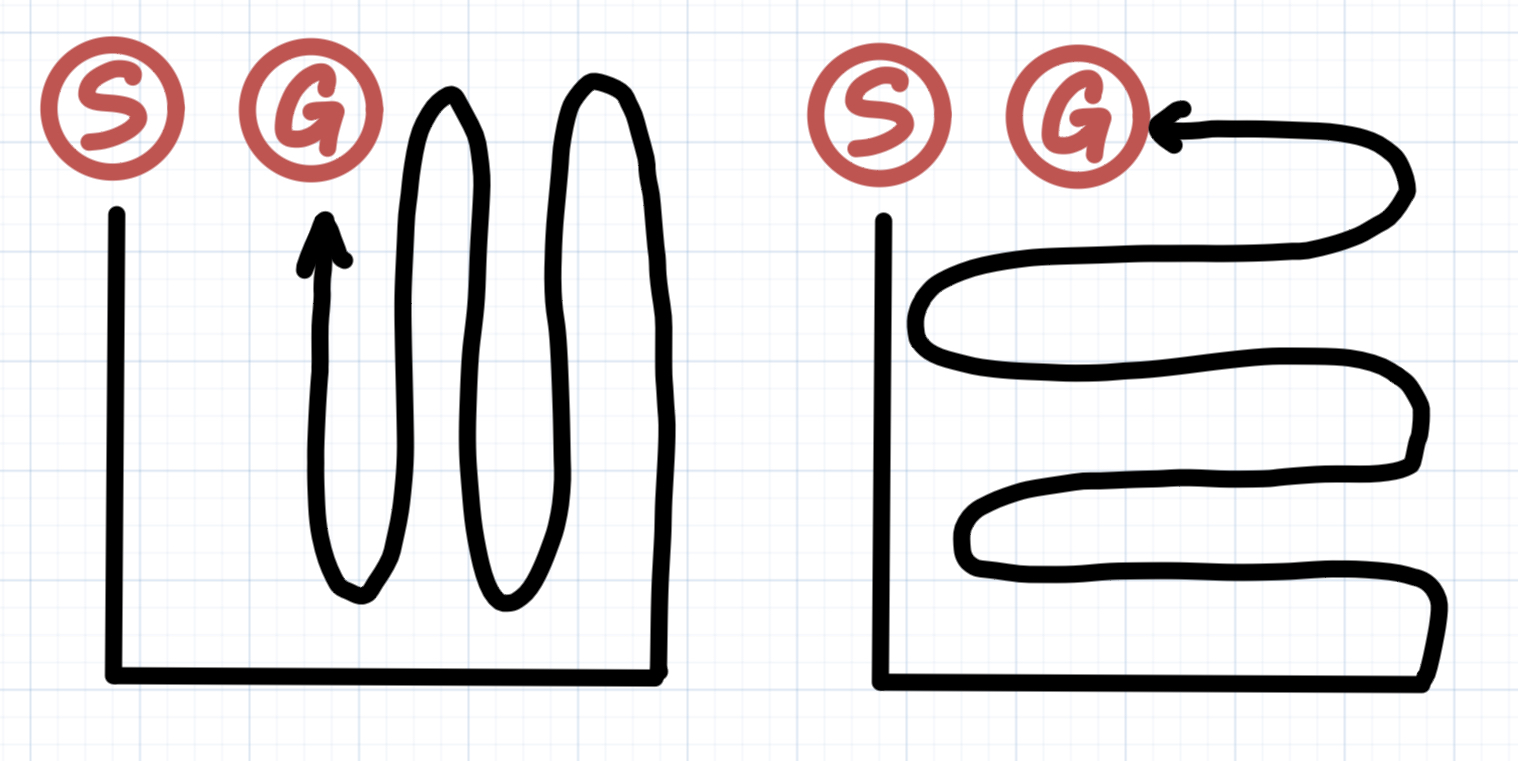
左ならC % 2 == 0で, 右ならR % 2 == 0なので, 結局K > 1 or R % 2 == 0 or C % 2 == 0なら可能.

蛇足

ハミルトン閉路みを感じて調べてみたけど, 巡回セールスマン問題の特殊ケースらしいからこのアプローチでは無理そう.

(参考: ハミルトン閉路問題 - Wikipedia)

提出コード(Python3🐍)

class PaintTheRoom:
    def canPaintEvenly(self,R,C,K):
        return['P','Cannot p'][(K>1)*R%2*C%2]+'aint'